Waves
Waves
Wave motion transfers energy from one point to another, usually without permanent displacement of the particles of the medium.
Learning Objectives
Describe process of energy and mass transfer during wave motion
Key Takeaways
Key Points
- A wave can be thought of as a disturbance or oscillation that travels through space-time, accompanied by a transfer of energy.
- The direction a wave propagates is perpendicular to the direction it oscillates for transverse waves.
- A wave does not move mass in the direction of propagation; it transfers energy.
Key Terms
- medium: The material or empty space through which signals, waves or forces pass.
- direction of propagation: The axis along which the wave travels.
- wave: A moving disturbance in the energy level of a field.
Vibrations and waves are extremely important phenomena in physics. In nature, oscillations are found everywhere. From the jiggling of atoms to the large oscillations of sea waves, we find examples of vibrations in almost every physical system. In physics a wave can be thought of as a disturbance or oscillation that travels through space-time, accompanied by a transfer of energy. Wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium —that is, with little or no associated mass transport. They consist, instead, of oscillations or vibrations around almost fixed locations.
The emphasis of the last point highlights an important misconception of waves. Waves transfer energy not mass. An easy way to see this is to imagine a floating ball a few yards out to sea. As the waves propagate (i.e., travel) towards the shore, the ball will not come towards the shore. It may come to shore eventually due to the tides, current or wind, but the waves themselves will not carry the ball with them. A wave only moves mass perpendicular to the direction of propagation—in this case up and down, as illustrated in the figure below:
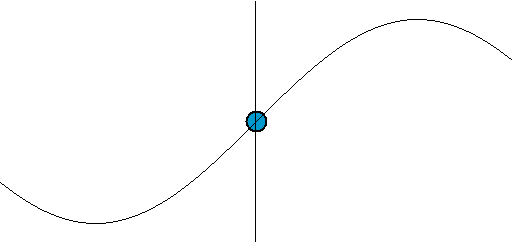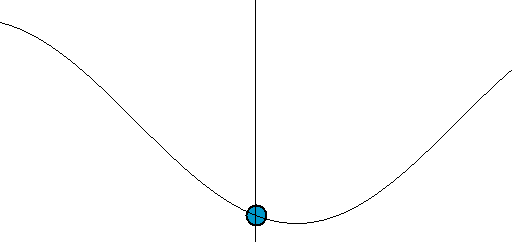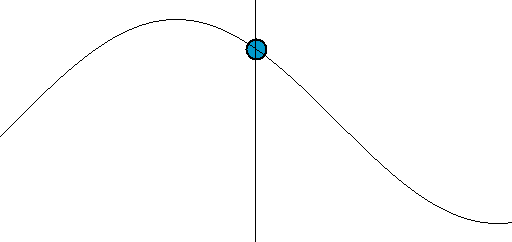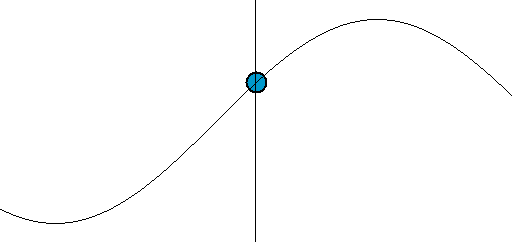
Wave motion: The point along the axis is analogous to the floating ball at sea. We notice that while it moves up and down it does not move in the direction of the wave’s propagation.
A wave can be transverse or longitudinal depending on the direction of its oscillation. Transverse waves occur when a disturbance causes oscillations perpendicular (at right angles) to the propagation (the direction of energy transfer). Longitudinal waves occur when the oscillations are parallel to the direction of propagation. While mechanical waves can be both transverse and longitudinal, all electromagnetic waves are transverse. Sound, for example, is a longitudinal wave.
The description of waves is closely related to their physical origin for each specific instance of a wave process. For example, acoustics is distinguished from optics in that sound waves are related to a mechanical rather than an electromagnetic (light) wave transfer caused by vibration. Therefore, concepts such as mass, momentum, inertia or elasticity become crucial in describing acoustic (as distinct from optic) wave processes. This difference in origin introduces certain wave characteristics particular to the properties of the medium involved. In this chapter we will closely examine the difference between longitudinal and transverse waves along with some of the properties they possess. We will also learn how waves are fundamental in describing motion of many applicable physical systems.
Transverse Waves
Transverse waves propagate through media with a speed [latex]\vec{\text{v}}_\text{w}[/latex] orthogonally to the direction of energy transfer.
Learning Objectives
Describe properties of the transverse wave
Key Takeaways
Key Points
- Transverse waves oscillate in the z-y plane but travel along the x axis.
- A transverse wave has a speed of propagation given by the equation v = fλ.
- The direction of energy transfer is perpendicular to the motion of the wave.
Key Terms
- wavelength: The length of a single cycle of a wave, as measured by the distance between one peak or trough of a wave and the next; it is often designated in physics as λ, and corresponds to the velocity of the wave divided by its frequency.
- trough: A long, narrow depression between waves or ridges.
- speed of propagation: The speed at which a wave moves through a medium.
- crest: The ridge or top of a wave.
- transverse wave: Any wave in which the direction of disturbance is perpendicular to the direction of travel.
- direction of propagation: The axis along which the wave travels.
A transverse wave is a moving wave that consists of oscillations occurring perpendicular (or right angled) to the direction of energy transfer. If a transverse wave is moving in the positive x-direction, its oscillations are in up and down directions that lie in the y–z plane. Light is an example of a transverse wave. For transverse waves in matter, the displacement of the medium is perpendicular to the direction of propagation of the wave. A ripple on a pond and a wave on a string are easily visualized transverse waves.
Transverse waves are waves that are oscillating perpendicularly to the direction of propagation. If you anchor one end of a ribbon or string and hold the other end in your hand, you can create transverse waves by moving your hand up and down. Notice though, that you can also launch waves by moving your hand side-to-side. This is an important point. There are two independent directions in which wave motion can occur. In this case, these are the y and z directions mentioned above. depicts the motion of a transverse wave. Here we observe that the wave is moving in t and oscillating in the x-y plane. A wave can be thought as comprising many particles (as seen in the figure) which oscillate up and down. In the figure we observe this motion to be in x-y plane (denoted by the red line in the figure). As time passes the oscillations are separated by units of time. The result of this separation is the sine curve we expect when we plot position versus time.
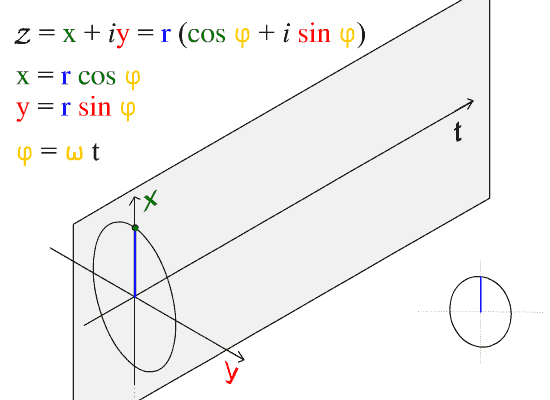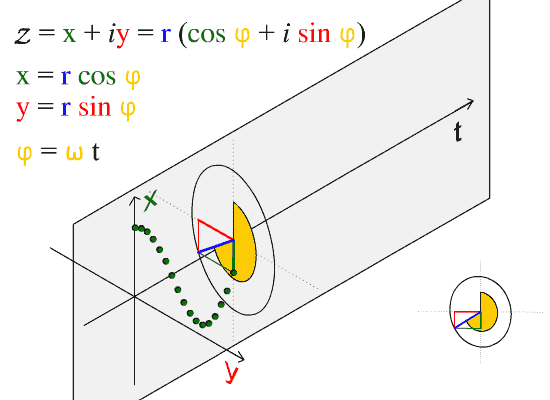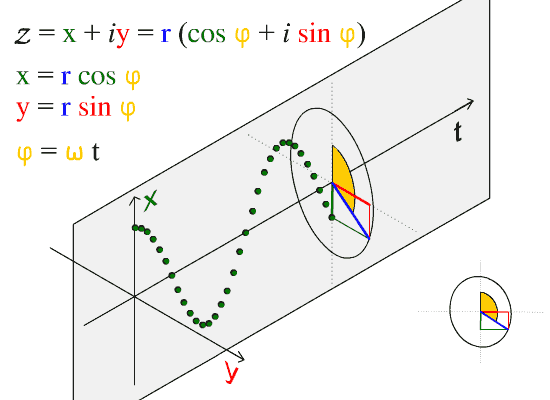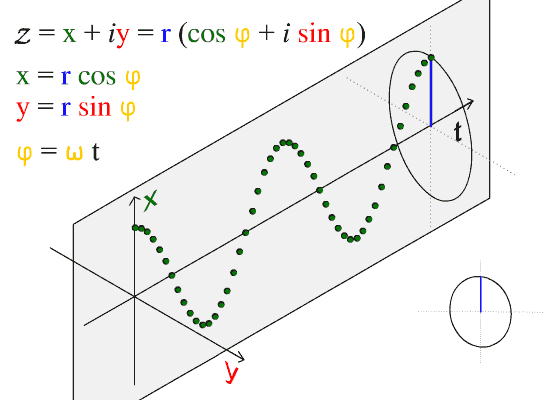
Sine Wave: The direction of propagation of this wave is along the t axis.
When a wave travels through a medium–i.e., air, water, etc., or the standard reference medium (vacuum)–it does so at a given speed: this is called the speed of propagation. The speed at which the wave propagates is denoted and can be found using the following formula:
[latex]\text{v}=\text{f} \lambda[/latex]
where v is the speed of the wave, f is the frequency , and is the wavelength. The wavelength spans crest to crest while the amplitude is 1/2 the total distance from crest to trough. Transverse waves have their applications in many areas of physics. Examples of transverse waves include seismic S (secondary) waves, and the motion of the electric (E) and magnetic (M) fields in an electromagnetic plane waves, which both oscillate perpendicularly to each other as well as to the direction of energy transfer. Therefore an electromagnetic wave consists of two transverse waves, visible light being an example of an electromagnetic wave.
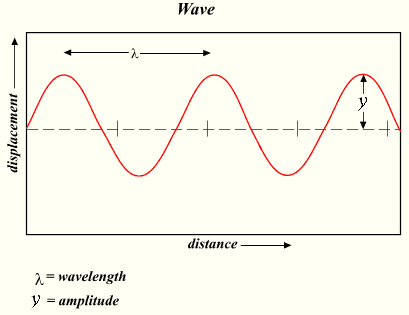
Wavelength and Amplitude: The wavelength is the distance between adjacent crests. The amplitude is the 1/2 the distance from crest to trough.
Longitudinal Waves
Longitudinal waves, sometimes called compression waves, oscillate in the direction of propagation.
Learning Objectives
Give properties and provide examples of the longitudinal wave
Key Takeaways
Key Points
- While longitudinal waves oscillate in the direction of propagation, they do not displace mass since the oscillations are small and involve an equilibrium position.
- The longitudinal ‘waves’ can be conceptualized as pulses that transfer energy along the axis of propagation.
- Longitudinal waves can be conceptualized as pressure waves characterized by compression and rarefaction.
Key Terms
- rarefaction: a reduction in the density of a material, especially that of a fluid
- Longitudinal: Running in the direction of the long axis of a body.
- compression: to increase in density; the act of compressing, or the state of being compressed; compaction
Longitudinal Waves
Longitudinal waves have the same direction of vibration as their direction of travel. This means that the movement of the medium is in the same direction as the motion of the wave. Some longitudinal waves are also called compressional waves or compression waves. An easy experiment for observing longitudinal waves involves taking a Slinky and holding both ends. After compressing and releasing one end of the Slinky (while still holding onto the end), a pulse of more concentrated coils will travel to the end of the Slinky.
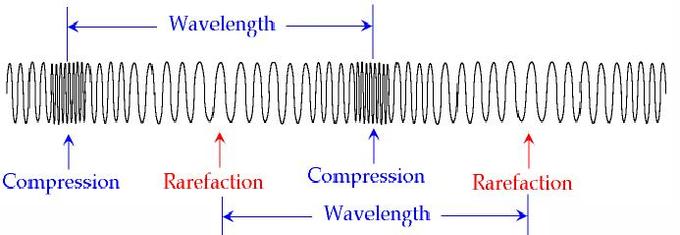
Longitudinal Waves: A compressed Slinky is an example of a longitudinal wave. The wave propagates in the same direction of oscillation.
Like transverse waves, longitudinal waves do not displace mass. The difference is that each particle which makes up the medium through which a longitudinal wave propagates oscillates along the axis of propagation. In the example of the Slinky, each coil will oscillate at a point but will not travel the length of the Slinky. It is important to remember that energy, in this case in the form of a pulse, is being transmitted and not the displaced mass.
Longitudinal waves can sometimes also be conceptualized as pressure waves. The most common pressure wave is the sound wave. Sound waves are created by the compression of a medium, usually air. Longitudinal sound waves are waves of alternating pressure deviations from the equilibrium pressure, causing local regions of compression and rarefaction. Matter in the medium is periodically displaced by a sound wave, and thus oscillates. When people make a sound, whether it is through speaking or hitting something, they are compressing the air particles to some significant amount. By doing so, they create transverse waves. When people hear sounds, their ears are sensitive to the pressure differences and interpret the waves as different tones.
Water Waves
Water waves can be commonly observed in daily life, and comprise both transverse and longitudinal wave motion.
Learning Objectives
Describe particle movement in water waves
Key Takeaways
Key Points
- The particles which make up a water wave move in circular paths.
- If the waves move slower than the wind above them, energy is transfered from the wind to the waves.
- The oscillations are greatest on the surface of the wave and become weaker deeper in the fluid.
Key Terms
- phase velocity: The velocity of propagation of a pure sine wave of infinite extent and infinitesimal amplitude.
- group velocity: The propagation velocity of the envelope of a modulated travelling wave, which is considered as the propagation velocity of information or energy contained in it.
- plane wave: A constant-frequency wave whose wavefronts (surfaces of constant phase) are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector.
Water waves, which can be commonly observed in our daily lives, are of specific interest to physicists. Describing detailed fluid dynamics in water waves is beyond the scope of introductory physics courses. Although we often observe water wave propagating in 2D, in this atom we will limit our discussion to 1D propagation.

Water waves: Surface waves in water
The uniqueness of water waves is found in the observation that they comprise both transverse and longitudinal wave motion. As a result, the particles composing the wave move in clockwise circular motion, as seen in. Oscillatory motion is highest at the surface and diminishes exponentially with depth. Waves are generated by wind passing over the surface of the sea. As long as the waves propagate slower than the wind speed just above the waves, there is an energy transfer from the wind to the waves. Both air pressure differences between the upwind and the lee side of a wave crest, as well as friction on the water surface by the wind (making the water to go into the shear stress), contribute to the growth of the waves.
In the case of monochromatic linear plane waves in deep water, particles near the surface move in circular paths, creating a combination of longitudinal (back and forth) and transverse (up and down) wave motions. When waves propagate in shallow water (where the depth is less than half the wavelength ), the particle trajectories are compressed into ellipses. As the wave amplitude (height) increases, the particle paths no longer form closed orbits; rather, after the passage of each crest, particles are displaced slightly from their previous positions, a phenomenon known as Stokes drift.
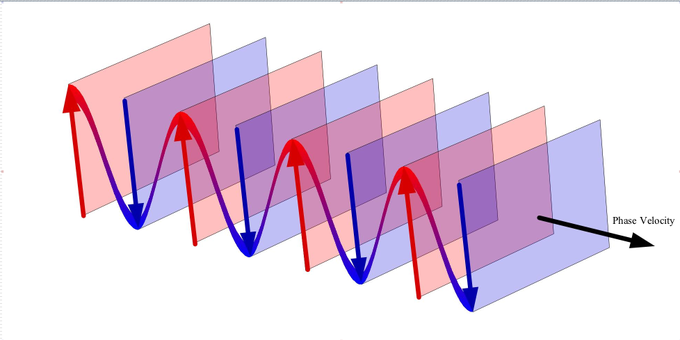
Plane wave: We see a wave propagating in the direction of the phase velocity. The wave can be thought to be made up of planes orthogonal to the direction of the phase velocity.
Since water waves transport energy, attempts to generate power from them have been made by utilizing the physical motion of such waves. Although larger waves are more powerful, wave power is also determined by wave speed, wavelength, and water density. Deep water corresponds with a water depth larger than half the wavelength, as is a common case in the sea and ocean. In deep water, longer-period waves propagate faster and transport their energy faster. The deep-water group velocity is half the phase velocity. In shallow water for wavelengths larger than about twenty times the water depth (as often found near the coast), the group velocity is equal to the phase velocity. These methods have proven viable in some cases but do not provide a fully sustainable form of renewable energy to date.

Water waves: The motion water waves causes particles to follow clockwise circular motion. This is a result of the wave having both transverse and longitudinal properties.
Wavelength, Freqency in Relation to Speed
Waves are defined by its frequency, wavelength, and amplitude among others. They also have two kinds of velocity: phase and group velocity.
Learning Objectives
Identify major characteristic properties of waves
Key Takeaways
Key Points
- The wavelength is the spatial period of the wave.
- The frequency of a wave refers to the number of cycles per unit time and is not to be confused with angular frequency.
- The phase velocity can be expressed as the product of wavelength and frequency.
Key Terms
- wave speed: The absolute value of the velocity at which the phase of any one frequency component of the wave travels.
- wavelength: The length of a single cycle of a wave, as measured by the distance between one peak or trough of a wave and the next; it is often designated in physics as λ, and corresponds to the velocity of the wave divided by its frequency.
- frequency: The quotient of the number of times n a periodic phenomenon occurs over the time t in which it occurs: f = n / t.
Characteristics of Waves
Waves have certain characteristic properties which are observable at first notice. The first property to note is the amplitude. The amplitude is half of the distance measured from crest to trough. We also observe the wavelength, which is the spatial period of the wave (e.g. from crest to crest or trough to trough). We denote the wavelength by the Greek letter [latex]\lambda[/latex].
The frequency of a wave is the number of cycles per unit time — one can think of it as the number of crests which pass a fixed point per unit time. Mathematically, we make the observation that,

Frequencies of different sine waves.: The red wave has a low frequency sine there is very little repetition of cycles. Conversely we say that the purple wave has a high frequency. Note that time increases along the horizontal.
[latex]\begin{equation} \text{f} = \frac{1}{\text{T}} \end{equation}[/latex]
where T is the period of oscillation. Frequency and wavelength can also be related-* with respects to a “speed” of a wave. In fact,
[latex]\begin{equation} \text{v} = \text{f} \lambda \end{equation}[/latex]
where v is called the wave speed, or more commonly,the phase velocity, the rate at which the phase of the wave propagates in space. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity.
Finally, the group velocity of a wave is the velocity with which the overall shape of the waves’ amplitudes — known as the modulation or envelope of the wave — propagates through space. In, one may see that the overall shape (or “envelope”) propagates to the right, while the phase velocity is negative.
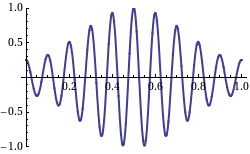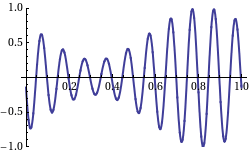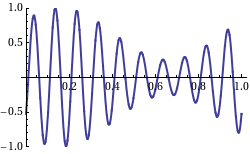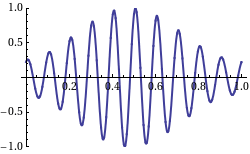
Fig 2: This shows a wave with the group velocity and phase velocity going in different directions. (The group velocity is positive and the phase velocity is negative. )
Energy Transportation
Waves transfer energy which can be used to do work.
Learning Objectives
Relate direction of energy and wave transportation
Key Takeaways
Key Points
- Waves which are more massive transfer more energy.
- Waves with greater velocities transfer more energy.
- Energy of a wave is transported in the direction of the waves transportation.
Key Terms
- energy: A quantity that denotes the ability to do work and is measured in a unit dimensioned in mass × distance²/time² (ML²/T²) or the equivalent.
- power: A measure of the rate of doing work or transferring energy.
- work: A measure of energy expended in moving an object; most commonly, force times displacement. No work is done if the object does not move.
Energy transportion is essential to waves. It is a common misconception that waves move mass. Waves carry energy along an axis defined to be the direction of propagation. One easy example is to imagine that you are standing in the surf and you are hit by a significantly large wave, and once you are hit you are displaced (unless you hold firmly to your ground!). In this sense the wave has done work (it applied a force over a distance). Since work is done over time, the energy carried by a wave can be used to generate power.

Water Wave: Waves that are more massive or have a greater velocity transport more energy.
Similarly we find that electromagnetic waves carry energy. Electromagnetic radiation (EMR) carries energy—sometimes called radiant energy—through space continuously away from the source (this is not true of the near-field part of the EM field). Electromagnetic waves can be imagined as a self-propagating transverse oscillating wave of electric and magnetic fields. EMR also carries both momentum and angular momentum. These properties may all be imparted to matter with which it interacts (through work). EMR is produced from other types of energy when created, and it is converted to other types of energy when it is destroyed. The photon is the quantum of the electromagnetic interaction, and is the basic “unit” or constituent of all forms of EMR. The quantum nature of light becomes more apparent at high frequencies (or high photon energy). Such photons behave more like particles than lower-frequency photons do.
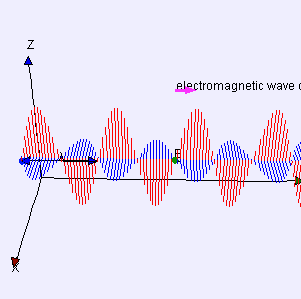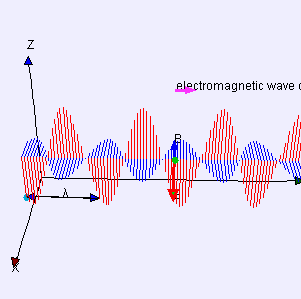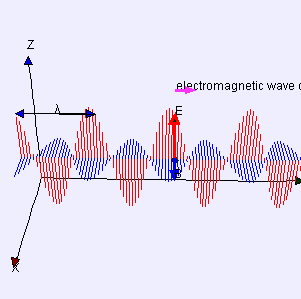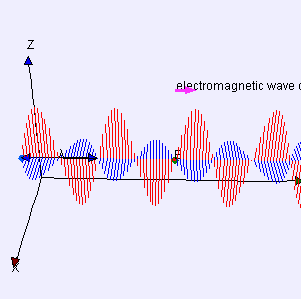
Electromagnetic Wave: Electromagnetic waves can be imagined as a self-propagating transverse oscillating wave of electric and magnetic fields. This 3D diagram shows a plane linearly polarized wave propagating from left to right.
In general, there is a relation of waves which states that the velocity ([latex]\text{v}[/latex]) of a wave is proportional to the frequency ([latex]\text{f}[/latex]) times the wavelength ([latex]\lambda[/latex]):
[latex]\text{v} = \text{f}\lambda[/latex]
We also know that classical momentum [latex]\text{p}[/latex] is given by [latex]\text{p} = \text{mv}[/latex] which relates to force via Newton’s second law: [latex]\text{F} = \frac{\text{dp}}{\text{dt}}[/latex]
EM waves with higher frequencies carry more energy. This is a direct result of the equations above. Since [latex]\text{v} \propto \text{f}[/latex] we find that higher frequencies imply greater velocity. If velocity is increased then we have greater momentum which implies a greater force (it gets a little bit tricky when we talk about particles moving close to the speed of light, but this observation holds in the classical sense). Since energy is the ability of an object to do work, we find that for [latex]\text{W} = \text{Fd}[/latex] a greater force correlates to more energy transfer. Again, this is an easy phenomenon to experience empirically; just stand in front of a faster wave and feel the difference!

