Radioactivity

Discovery of Radioactivity

Becquerel accidentally found that a uranium-rich mineral emitted invisible, penetrating rays that could darken a photographic plate.

Becquerel’s Pitchblende

In 1896, the French physicist Antoine Henri Becquerel accidentally found that a uranium-rich mineral called pitchblende emitted invisible, penetrating rays that could darken a photographic plate enclosed in an opaque envelope. While working on phosphorescent materials, he happened to place the pitchblende on black paper that he had used to cover a piece of film. When he looked more carefully, he noticed that the film had lots of patches on it, and that this did not happen when other elements were placed on the paper. He eventually concluded that some rays must be coming out of the uranium crystals to produce this effect.

This means that rays carry energy, but pitchblende emits them continuously without any energy input. This is an apparent violation of the law of conservation of energy. It was soon evident that Becquerel’s rays originated in the nuclei of the atoms.

The emission of these rays is called nuclear radioactivity, or simply radioactivity. The rays are called nuclear radiation. A nucleus that spontaneously destroys part of its mass to emit radiation is said to decay. A substance or object that emits nuclear radiation is said to be radioactive. Becquerel found radiation to be associated with certain elements, such as uranium. Uranium is radioactive whether it is in the form of an element or compound. In addition, radiation does not vary with temperature, pressure, or ionization state of the uranium atom. Since all of these factors affect electrons in an atom, the radiation cannot come from electron transitions, as atomic spectra do.

Marie and Pierre Curie

In 1898, Marie Curie began her doctoral study of Becquerel’s rays. She and her husband, Pierre, soon discovered two new radioactive elements, which she named polonium, after her native land of Poland, and radium, because it radiates. These two new elements filled holes in the periodic table and displayed much higher levels of radioactivity than uranium. Over four years, working under poor conditions and spending their own funds, the Curies processed more than a ton of uranium ore to isolate a mere gram of radium salt.

Pierre and Marie Curie: Pierre and Marie Curie in their Paris laboratory, before 1907.

Radium became highly desirable because it was about two million times as radioactive as uranium. The Curies’ radium salt glowed visibly from the radiation. This radiation took its toll on them and other unaware researchers, though.

Shortly after Marie completed her PhD, both Curies and Becquerel shared the 1903 Nobel Prize in Physics for their work on radioactivity. Awarded the 1911 Nobel Prize in Chemistry for her discovery of two new elements, Curie remains the only person to win Nobel Prizes in both physics and chemistry. Marie’s radioactive fingerprints on some pages of her notebooks can still expose film.

Marie suffered from radiation-induced lesions and died of leukemia, likely caused by radiation. She was active in research almost until her death in 1934. The following year, her daughter and son-in-law, Irene and Frederic Joliot-Curie, were awarded the Nobel Prize in Chemistry for their discovery of artificially induced radiation.

Modes of Radioactive Decay

Radioactive decay occurs when an unstable atomic nucleus emits particles or light waves.

Radioactivity

Radioactive decay occurs when an unstable atomic nucleus loses energy by emitting energy in the form of emitted particles or electromagnetic waves, called radiation. Isotopes are atoms of the same element (thereby having the same number of protons) which differ in the number of neutrons in their nucleus. Some isotopes of a given element are more unstable than others, causing a nuclear reaction which releases energy to achieve a more stable nuclear configuration. Such isotopes are radioactive, and are referred to as “radioisotopes.”

Types of Decay

There are many types of emmitted particles and radiation that radioisotopes produce when they decay. The types we will discuss here are: alpha, beta, and gamma (listed in increasing ability to penetrate matter). Alpha decay is seen only in heavier elements greater than atomic number 52, tellurium. The other two types of decay are seen in all of the elements.

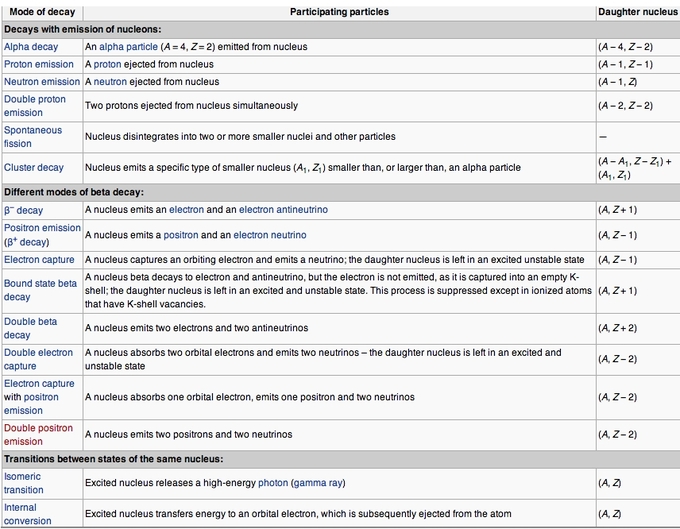
Table of modes of radioactive decay: Radionuclides can undergo a number of different reactions, summarized here. A nucleus with mass number A and atomic number Z is represented as (A, Z). The column “Daughter nucleus” indicates the difference between the new nucleus and the original nucleus. Thus, (A − 1, Z) means that the mass number is one less than before, but the atomic number didn’t change.

Alpha, Beta, Gamma Composition

Alpha particles carry a positive charge, beta particles carry a negative charge, and gamma rays are neutral. Alpha particles have greater mass than beta particles. By passing alpha particles through a very thin glass window and trapping them in a discharge tube, researchers found that alpha particles are equivalent to helium (He) nuclei. Other experiments showed the similarity between classical beta radiation and cathode rays; they are both streams of electrons. Likewise, gamma radiation and X-rays were found to be similar high-energy electromagnetic radiation.

The three types of radiation have different levels of penetrating power. Penetrating power refers to the energy with which the radiation particles are ejected from the atom. The higher the energy, the more the particles or light produced by radioactive decay will penetrate a substance.

Penetration of the modes of decay: Alpha particles can be completely stopped by a sheet of paper. Beta particles can be stopped by aluminum shielding. Gamma rays can only be reduced by much more substantial mass, such as a very thick layer of lead.

Alpha Decay

An alpha particle (α\alpha) is made up of two protons and two neutrons bound together. This type of radiation has a positive charge (due to the presence of two protons). An alpha particle is sometimes represented using the chemical symbol He²⁺, because it has the same structure as a helium atom missing its two electrons—hence the overall charge of +2. Their massive size (compared to beta particles, for instance) means alpha particles have very low penetration power. Penetration power describes how easily the particles can pass through another material. Since alpha particles have a low penetration power, the outside layer of the human skin, for example, can block these particles.

Alpha decay occurs because the nucleus of a radioisotope has too many protons. A nucleus with too many protons causes repulsion between these like charges. To reduce this repulsion, the nucleus emits an α particle. Examples of this can be seen in the decay of americium (Am) to neptunium (Np).

Beta Decay

In radioactive nuclei with too many neutrons, a neutron can be converted into an electron, called beta particle. Beta particles (β) have a higher penetration power than alpha particles (they are able to pass through thicker materials such as paper).

During beta decay, the number of neutrons in the atom decreases by one, and the number of protons increases by one. Effectively, a neutron was converted into a proton in the decaying nucleus, in the process releasing a beta particle. Since the number of protons before and after the decay is different, the atom has changed into a different element.

Gamma Decay

Some decay reactions release energy in the form of electromagnetic waves called gamma rays. Gamma radiation (γ) is part of the electromagnetic spectrum, just like visible light. However, unlike visible light, humans cannot see gamma rays, because they have a much higher frequency and energy than visible light. Gamma radiation has no mass or charge. This type of radiation is able to penetrate most common substances, including metals. The only substances that can absorb this radiation are thick lead and concrete.

Gamma decay reactions occur if the energy of the radioisotope’s nucleus is too high, and the resulting atomic number and atomic mass remain unchanged during the course of the reaction.

Rate of Radioactive Decay

Radioactive decay rate is exponential and is characterized by constants, such as half-life, as well the activity and number of particles.

Decay Rate

The decay rate of a radioactive substance is characterized by the following constant quantities:

• The half-life (t_1/2) is the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value.
• The mean lifetime (τ, “tau”) is the average lifetime of a radioactive particle before decay.
• The decay constant (λ, “lambda”) is the inverse of the mean lifetime.

Although these are constants, they are associated with statistically random behavior of populations of atoms. Predictions using these constants are less accurate for small number of atoms.

There are also time-variable quantities to consider:

• Total activity (A) is number of decays per unit time of a radioactive sample.
• Number of particles (N) is the total number of particles in the sample.
• Specific activity (SA) number of decays per unit time per amount of substance of the sample at time set to zero (t = 0). “Amount of substance” can be the mass, volume, or moles of the initial sample.

Radioactivity is one very frequent example of exponential decay. The law of radioactive decay describes the statistical behavior of a large number of nuclides, rather than individual ones. In the following relation, the number of nuclides or nuclide population, N, is of course a natural number. Given a sample of a particular radioisotope, the number of decay events, −dN, expected to occur in a small interval of time, dt, is proportional to the number of atoms present N, that is:

[latex]-\frac { \text{dN} }{ \text{dt} } \propto \text{N}[/latex]

Exponential decay: A quantity undergoing exponential decay. Larger decay constants make the quantity vanish much more rapidly. This plot shows decay for decay constants of 25, 5, 1, 1/5, and 1/25 for x from 0 to 5.

Particular radionuclides decay at different rates, so each has its own decay constant, λ. The expected decay [latex]\frac {-\text{dN}}{\text{N}}[/latex] is proportional to an increment of time, dt. The constant [latex]\lambda[/latex] is put in place to make the two sides equal:

[latex]-\frac { \text{dN} }{ \text{N} } =\quad \lambda \text{dt}[/latex]

The negative sign indicates that N decreases as time increases, as each decay event follows one after another. The solution to this first-order differential equation is the function:

[latex]\text{N}={\text{N}}_{0}{\text{e}}^{-\lambda \text{t}}[/latex]

Here, N₀ is the value of N at time t = 0.

The SI unit of radioactive activity is the becquerel (Bq), in honor of the scientist Henri Becquerel. One Bq is defined as one transformation, decay, or disintegration per second. Since sensible sizes of radioactive material contain many atoms, a Bq is a tiny measure of activity; amounts giving activities on the order of GBq (gigabecquerel, 1 x 10⁹ decays per second) or TBq (terabecquerel, 1 x 10¹² decays per second) are commonly used.

Another unit of radioactivity is the curie, Ci, which was originally defined as the amount of radium emanation (radon-222) in equilibrium with one gram of pure radium, isotope Ra-226. At present, it is equal, by definition, to the activity of any radionuclide decaying with a disintegration rate of 3.7 × 10¹⁰ Bq, so that 1 curie (Ci) = 3.7 × 10¹⁰ Bq. The use of Ci is currently discouraged by the SI. Low activities are also measured in disintegrations per minute (dpm).

Half-Life of Radioactive Decay

The half-life is a parameter for the rate of decay that is related to the decay constant by: [latex]{\text{t}}_{\frac{1}{2}}=\frac{\text{ln}2}{\lambda}[/latex].

Decay Rates

Radioactive decay is a random process at the single- atom level; is impossible to predict exactly when a particular atom will decay. However, the chance that a given atom will decay is constant over time. For a large number of atoms, the decay rate for the collection as a whole can be computed from the measured decay constants of the nuclides, or, equivalently, from the half-lives.

Radioactive decay simulation: A simulation of many identical atoms undergoing radioactive decay, starting with four atoms (left) and 400 atoms (right). The number at the top indicates how many half-lives have elapsed

Given a sample of a particular radionuclide, the half-life is the time taken for half of its atoms to decay. The following equation is used to predict the number of atoms (N) of a a given radioactive sample that remain after a given time (t):

[latex]\text{N}={\text{N}}_{0}{\text{e}}^{-\lambda \text{t}}[/latex]

In this equation, λ, pronounced “lambda,” is the decay constant, which is the inverse of the mean lifetime, and N₀ is the value of N at t=0. The equation indicates that the decay constant λ has units of t^-1_.

The half-life is related to the decay constant. If you set N = [latex]\frac{\text{N}_0}{2}[/latex] and t = t_1/2, you obtain the following:

[latex]{\text{t}}_{1/2}=\frac{\text{ln}2}{\lambda}[/latex]

This relationship between the half-life and the decay constant shows that highly radioactive substances are quickly spent, while those that radiate weakly endure longer. Half-lives vary widely; the half-life of ²⁰⁹Bi is 1019 years, while unstable nuclides can have half-lives that have been measured as short as 10⁻²³ seconds.

Dating Using Radioactive Decay

Radiometric dating is used to date materials using the decay rate of a radioactive isotope.

Radiometric Dating

Radiometric dating, often called radioactive dating, is a technique used to determine the age of materials such as rocks. It is based on a comparison between the observed abundance of a naturally occurring radioactive isotope and its decay products, using known decay rates. It is the principal source of information about the absolute age of rocks and other geological features, including the age of the Earth itself, and it can be used to date a wide range of natural and man-made materials.

The best-known radiometric dating techniques include radiocarbon dating, potassium-argon dating, and uranium-lead dating. By establishing geological timescales, radiometric dating provides a significant source of information about the ages of fossils and rates of evolutionary change, and it is also used to date archaeological materials, including ancient artifacts. The different methods of radiometric dating are accurate over different timescales, and they are useful for different materials.

Decay

After one half-life has elapsed, one half of the atoms of the nuclide in question will have decayed into a “daughter” nuclide, or decay product. In many cases, the daughter nuclide is radioactive, resulting in a decay chain. This chain eventually ends with the formation of a stable, nonradioactive daughter nuclide. Each step in such a chain is characterized by a distinct half-life. In these cases, the half-life of interest in radiometric dating is usually the longest one in the chain. This half-life will be the rate-limiting factor in the ultimate transformation of the radioactive nuclide into its stable daughter(s).

Lead decay chain: Example of a radioactive decay chain from lead-212 (212Pb) to lead-208 (208Pb). Each parent nuclide spontaneously decays into a daughter nuclide (the decay product) via an α decay or a β decay. The final decay product, lead-208 (208Pb), is stable and can no longer undergo spontaneous radioactive decay.

Systems that have been exploited for radiometric dating have half-lives ranging from only about 10 years (e.g., tritium) to over 100 billion years (e.g., Samarium-147). However, in general, the half-life of a nuclide depends solely on its nuclear properties and is essentially a constant. Therefore, in any material containing a radioactive nuclide, the proportion of the original nuclide to its decay products changes in a predictable way as the original nuclide decays over time. This predictability allows the relative abundances of related nuclides to be used as a clock to measure the time it takes for the parent atom to decay into the daughter atom(s).

Accuracy and Contamination

Accurate radiometric dating generally requires that:

• The parent has a long enough half-life to ensure the parent will be present in significant amounts at the time of measurement.
• The half-life of the parent is accurately known.
• Enough of the daughter product is produced to be accurately measured and distinguished from the initial amount of the daughter present in the material.

The mathematical expression that relates radioactive decay to geologic time is:

[latex]\text{D}={\text{D}}_{0}+\text{N}(\text{t})({\text{e}}^{\lambda \text{t}}-1)[/latex]

Here, t is age of the sample; D is number of atoms of the daughter isotope in the sample; D₀ is number of atoms of the daughter isotope in the original composition; N is number of atoms of the parent isotope in the sample at time t (the present), given by N(t) = N_oe^-λt; and λ is the decay constant of the parent isotope, equal to the inverse of the radioactive half-life of the parent isotope times the natural logarithm of 2.