8.1 What Are the Chances?

Brad Griffith; Lisa Friesen

8.1 What Are the Chances?

8.1: What Are the Chances?

8.1.1: Fundamentals of Probability

Probability is the branch of mathematics that deals with the likelihood that certain outcomes will occur. There are five basic rules, or axioms, that one must understand while studying the fundamentals of probability.

Learning Objective

Explain the most basic and most important rules in determining the probability of an event

Key Takeaways

Key Points

Probability is a number that can be assigned to outcomes and events. It always is greater than or equal to zero, and less than or equal to one.
The sum of the probabilities of all outcomes must equal $1$ .
If two events have no outcomes in common, the probability that one or the other occurs is the sum of their individual probabilities.
The probability that an event does not occur is $1$ minus the probability that the event does occur.
Two events $A$ and $B$ are independent if knowing that one occurs does not change the probability that the other occurs.

Key Terms

experiment: Something that is done that produces measurable results, called outcomes.
outcome: One of the individual results that can occur in an experiment.
event: A subset of the sample space.
sample space: The set of all outcomes of an experiment.

In discrete probability, we assume a well-defined experiment, such as flipping a coin or rolling a die. Each individual result which could occur is called an outcome. The set of all outcomes is called the sample space, and any subset of the sample space is called an event.

For example, consider the experiment of flipping a coin two times. There are four individual outcomes, namely $HH, HT, TH, TT$ . The sample space is thus ${HH, HT, TH, TT}$ . The event “at least one heads occurs” would be the set ${HH, HT, TH}$ . If the coin were a normal coin, we would assign the probability of 1/4 to each outcome.

In probability theory, the probability $P$ of some event $E$ , denoted $P (E)$ , is usually defined in such a way that $P$ satisfies a number of axioms, or rules. The most basic and most important rules are listed below.

Probability Rules

Probability is a number. It is always greater than or equal to zero, and less than or equal to one. This can be written as $0 \leq P (A) \geq 1$ . An impossible event, or an event that never occurs, has a probability of $0$ . An event that always occurs has a probability of $1$ . An event with a probability of $0.5$ will occur half of the time.

The sum of the probabilities of all possibilities must equal $1$ . Some outcome must occur on every trial, and the sum of all probabilities is 100%, or in this case, $1$ . This can be written as $P (S) = 1$ , where $S$ represents the entire sample space.

If two events have no outcomes in common, the probability that one or the other occurs is the sum of their individual probabilities. If one event occurs in 30% of the trials, a different event occurs in 20% of the trials, and the two cannot occur together (if they are disjoint), then the probability that one or the other occurs is 30%+20%=50%. This is sometimes referred to as the addition rule, and can be simplified with the following: $P (A or B) = P (A) + P (B)$ . The word “or” means the same thing in mathematics as the union, which uses the following symbol: $\cup$ . Thus when $A$ and $B$ are disjoint, we have $P (A \cup B) = P (A) + P (B)$ . The probability that an event does not occur is $1$ minus the probability that the event does occur. If an event occurs in 60% of all trials, it fails to occur in the other 40%, because 100%−60%=40%. The probability that an event occurs and the probability that it does not occur always add up to 100%, or $1$ . These events are called complementary events, and this rule is sometimes called the complement rule. It can be simplified with $P (A^{c}) = 1 - P (A)$ , where $A^{c}$ is the complement of $A$ .

Two events $A$ and $B$ are independent if knowing that one occurs does not change the probability that the other occurs. This is often called the multiplication rule. If $A$ and $B$ are independent, then $P (A and B) = P (A) P (B)$ . The word “and” in mathematics means the same thing in mathematics as the intersection, which uses the following symbol: $\cap$ . Therefore when $A$ and $B$ are independent, we have $P (A \cap B) = P (A) P (B)$ .

Extension of the Example

Die

Die

Dice are often used when learning the rules of probability.

Elaborating on our example above of flipping two coins, assign the probability $1 / 4$ to each of the $4$ outcomes. We consider each of the five rules above in the context of this example.

Note that each probability is $1 / 4$ , which is between $0$ and $1$ .
Note that the sum of all the probabilities is $1$ , since $\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = 1$ .
Suppose $A$ is the event exactly one head occurs, and B is the event exactly two tails occur. Then $A = {HT, TH}$ and $B = {TT}$ are disjoint. Also, $P(A\cup B)=\frac{3}{4}=\frac{2}{4}+\frac{1}{4}=P(A)+P(B)$ .
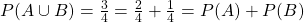The probability that no heads occurs is $1 / 4$ , which is equal to $1 - 3 / 4$ . So if $A = {HT, TH, HH}$ is the event that a head occurs, we have $P (A^{c}) = \frac{1}{4} = 1 - \frac{3}{4} = 1 - P (A)$ .
If $A$ is the event that the first flip is a heads and $B$ is the event that the second flip is a heads, then $A$ and $B$ are independent. We have $A = {HT, HH}$ and $B = TH, HH$ and $A \cap B = HH$ . Note that $P (A \cap B) = \frac{1}{4} = \frac{1}{2} \cdot \frac{1}{2} = P (A) P (B)$ .

8.1.2: Conditional Probability

The conditional probability of an event is the probability that an event will occur given that another event has occurred.

Learning Objective

Explain the significance of Bayes’ theorem in manipulating conditional probabilities

Key Takeaways

Key Points

The conditional probability $P (B ∣ A)$ of an event $B$ , given an event $A$ , is defined by: 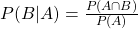$P(B|A)=\frac{P(A\cap B)}{P(A)}$ , when $P (A) > 0$ .
If the knowledge that event $A$ occurs does not change the probability that event $B$ occurs, then $A$ and $B$ are independent events, and thus, $P (B ∣ A) = P (B)$ .
Mathematically, Bayes’ theorem gives the relationship between the probabilities of $A$ and $B, P (A)$ and $P (B)$ , and the conditional probabilities of $A$ given $B$ and $B$ given $A, P (A \cap B)$ and $P (B \cap A)$ . In its most common form, it is: $P (A \cap B) = \frac{P (B ∣ A) P (A)}{P (B)}$ .

Key Terms

conditional probability: The probability that an event will take place given the restrictive assumption that another event has taken place, or that a combination of other events has taken place
independent: Not dependent; not contingent or depending on something else; free.

Probability of B Given That A Has Occurred

Our estimation of the likelihood of an event can change if we know that some other event has occurred. For example, the probability that a rolled die shows a $2$ is $1 / 6$ without any other information, but if someone looks at the die and tells you that is is an even number, the probability is now $1 / 3$ that it is a $2$ . The notation $P (B ∣ A)$ indicates a conditional probability, meaning it indicates the probability of one event under the condition that we know another event has happened. The bar “ $∣$ ” can be read as “given”, so that $P (B ∣ A)$ is read as “the probability of $B$ given that $A$ has occurred”.

The conditional probability $P (B ∣ A)$ of an event $B$ , given an event $A$ , is defined by:

$P (B ∣ A) = \frac{P (A \cap B)}{P (A)}$

When $P (A) > 0$ . Be sure to remember the distinct roles of $B$ and $A$ in this formula. The set after the bar is the one we are assuming has occurred, and its probability occurs in the denominator of the formula.

Example

Suppose that a coin is flipped 3 times giving the sample space:

$S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}$

Each individual outcome has probability $1 / 8$ . Suppose that $B$ is the event that at least one heads occurs and $A$ is the event that all 3 coins are the same. Then the probability of $B$ given $A$ is $1 / 2$ , since $A \cap B = {HHH}$ which has probability $1 / 8$ and $A = {HHH, TTT}$ which has probability $2 / 8$ , and $\frac{1 / 8}{2 / 8} = \frac{1}{2}$ .

Independence

The conditional probability $P (B ∣ A)$ is not always equal to the unconditional probability $P (B)$ . The reason behind this is that the occurrence of event $A$ may provide extra information that can change the probability that event $B$ occurs. If the knowledge that event $A$ occurs does not change the probability that event $B$ occurs, then $A$ and $B$ are independent events, and thus, $P (B ∣ A) = P (B)$ .

Bayes’ Theorem

In probability theory and statistics, Bayes’ theorem (alternatively Bayes’ law or Bayes’ rule) is a result that is of importance in the mathematical manipulation of conditional probabilities. It can be derived from the basic axioms of probability.

Mathematically, Bayes’ theorem gives the relationship between the probabilities of $A$ and $B$ , $P (A)$ and $P (B)$ , and the conditional probabilities of $A$ given $B$ and $B$ given $A$ . In its most common form, it is:

$P (A ∣ B) = \frac{P (B ∣ A) P (A)}{P (B)}$

This may be easier to remember in this alternate symmetric form:

$\frac{P (A ∣ B)}{P (B ∣ A)} = \frac{P (A)}{P (B)}$

Example

Suppose someone told you they had a nice conversation with someone on the train. Not knowing anything else about this conversation, the probability that they were speaking to a woman is 50%. Now suppose they also told you that this person had long hair. It is now more likely they were speaking to a woman, since women in in this city are more likely to have long hair than men. Bayes’s theorem can be used to calculate the probability that the person is a woman.

To see how this is done, let $W$ represent the event that the conversation was held with a woman, and $L$ denote the event that the conversation was held with a long-haired person. It can be assumed that women constitute half the population for this example. So, not knowing anything else, the probability that $W$ occurs is $P (W) = 0.5$ .

Suppose it is also known that 75% of women in this city have long hair, which we denote as $P (L ∣ W) = 0.75$ . Likewise, suppose it is known that 25% of men in this city have long hair, or $P (L ∣ M) = 0.25$ , where $M$ is the complementary event of $W$ , i.e., the event that the conversation was held with a man (assuming that every human is either a man or a woman).

Our goal is to calculate the probability that the conversation was held with a woman, given the fact that the person had long hair, or, in our notation, $P (W ∣ L)$ . Using the formula for Bayes’s theorem, we have:

$P (W ∣ L) = \frac{P (L ∣ W) P (W)}{P (L)} = \frac{P (L ∣ W) P (W)}{P (L ∣ W) P (W) + P (L ∣ M) P (M)} = \frac{0.75 \cdot 0.5}{0.75 \cdot 0.5 + 0.25 \cdot 0.5} = 0.75$

8.1.3: Unions and Intersections

Union and intersection are two key concepts in set theory and probability.

Learning Objective

Give examples of the intersection and the union of two or more sets

Key Takeaways

Key Points

The union of two or more sets is the set that contains all the elements of the two or more sets. Union is denoted by the symbol $\cup$
The general probability addition rule for the union of two events states that $P (A \cup B) = P (A) + P (B) - P (A \cap B)$ , where $A \cap B$ is the intersection of the two sets.
The addition rule can be shortened if the sets are disjoint: $P (A \cup B) = P (A) + P (B)$ . This can even be extended to more sets if they are all disjoint: $P (A \cup B \cup C) = P (A) + P (B) + P (C)$ .
The intersection of two or more sets is the set of elements that are common to every set. The symbol $\cap$ is used to denote the intersection.
When events are independent, we can use the multiplication rule for independent events, which states that $P (A \cap B) = P (A) P (B)$ .

Key Terms

independent: Not contingent or dependent on something else.
disjoint: Having no members in common; having an intersection equal to the empty set.

Probability uses the mathematical ideas of sets, as we have seen in the definition of both the sample space of an experiment and in the definition of an event. In order to perform basic probability calculations, we need to review the ideas from set theory related to the set operations of union, intersection, and complement.

Union

The union of two or more sets is the set that contains all the elements of each of the sets; an element is in the union if it belongs to at least one of the sets. The symbol for union is $\cup$ , and is associated with the word “or”, because $A \cup B$ is the set of all elements that are in $A$ or $B$ (or both.) To find the union of two sets, list the elements that are in either (or both) sets. In terms of a Venn Diagram, the union of sets $A$ and $B$ can be shown as two completely shaded interlocking circles.

Union of Two Sets

Union of Two Sets: The shaded Venn Diagram shows the union of set $A$ (the circle on left) with set $B$ (the circle on the right). It can be written shorthand as $A \cup B$

In symbols, since the union of $A$ and $B$ contains all the points that are in $A$ or $B$ or both, the definition of the union is:

$A \cup B = {x : x \in A or x \in B}$

For example, if $A = {1, 3, 5, 7}$ and $B = {1, 2, 4, 6}$ , then $A \cup B = {1, 2, 3, 4, 5, 6, 7}$ . Notice that the element 1 is not listed twice in the union, even though it appears in both sets $A$ and $B$ . This leads us to the general addition rule for the union of two events:

$P (A \cup B) = P (A) + P (B) - P (A \cap B)$

Where $P (A \cap B)$ is the intersection of the two sets. We must subtract this out to avoid double counting of the inclusion of an element.

If sets $A$ and $B$ are disjoint, however, the event $A \cap B$ has no outcomes in it, and is an empty set denoted as ∅, which has a probability of zero. So, the above rule can be shortened for disjoint sets only:

$P (A \cup B) = P (A) + P (B)$

This can even be extended to more sets if they are all disjoint:

$P (A \cup B \cup C) = P (A) + P (B) + P (C)$

Intersection

The intersection of two or more sets is the set of elements that are common to each of the sets. An element is in the intersection if it belongs to all of the sets. The symbol for intersection is $\cap$ , and is associated with the word “and”, because $A \cap B$ is the set of elements that are in $A$ and $B$ simultaneously. To find the intersection of two (or more) sets, include only those elements that are listed in both (or all) of the sets. In terms of a Venn Diagram, the intersection of two sets $A$ and $B$ can be shown at the shaded region in the middle of two interlocking circles .

Intersection of Two Sets

Set A is the circle on the left, set B is the circle on the right, and the intersection of A and B, or $A \cap B$ , is the shaded portion in the middle.

In mathematical notation, the intersection of $A$ and $B$ is written as $A \cap B = {x : x \in A$ and $x \in B}$ . For example, if $A = {1, 3, 5, 7}$ and $B = {1, 2, 4, 6}$ , then $A \cap B = {1}$ because $1$ is the only element that appears in both sets $A$ and $B$ .

When events are independent, meaning that the outcome of one event doesn’t affect the outcome of another event, we can use the multiplication rule for independent events, which states:

$P (A \cap B) = P (A) P (B)$

For example, let’s say we were tossing a coin twice, and we want to know the probability of tossing two heads. Since the first toss doesn’t affect the second toss, the events are independent. Say is the event that the first toss is a heads and $B$ is the event that the second toss is a heads, then $P(A\cap B)=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$ .

8.1.4: Complementary Events

The complement of A is the event in which A does not occur.

Learning Objectives

Explain an example of a complementary event

Key Takeaways

Key Points

The complement of an event $A$ is usually denoted as $A'$ , $A^{c}$ or $\bar{A}$ $\bar{A}$ .
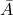An event and its complement are mutually exclusive, meaning that if one of the two events occurs, the other event cannot occur.
An event and its complement are exhaustive, meaning that both events cover all possibilities.

Key Terms

exhaustive: including every possible element
mutually exclusive: describing multiple events or states of being such that the occurrence of any one implies the non-occurrence of all the others

What are Complementary Events?

In probability theory, the complement of any event $A$ is the event $[not A]$ , i.e. the event in which $A$ does not occur. The event $A$ and its complement $[not A]$ are mutually exclusive and exhaustive, meaning that if one occurs, the other does not, and that both groups cover all possibilities. Generally, there is only one event $B$ such that $A$ and $B$ are both mutually exclusive and exhaustive; that event is the complement of $A$ . The complement of an event $A$ is usually denoted as $A'$ , $A^{c}$ or $\bar{A}$ $\bar{A}$ .

Simple Examples

A common example used to demonstrate complementary events is the flip of a coin. Let’s say a coin is flipped and one assumes it cannot land on its edge. It can either land on heads or on tails. There are no other possibilities (exhaustive), and both events cannot occur at the same time (mutually exclusive). Because these two events are complementary, we know that P(heads) + P(tails)=1.

Coin Flip

Coin Flip

Often in sports games, such as tennis, a coin flip is used to determine who will serve first because heads and tails are complementary events.

Another simple example of complementary events is picking a ball out of a bag. Let’s say there are three plastic balls in a bag. One is blue and two are red. Assuming that each ball has an equal chance of being pulled out of the bag, we know that $P (blue) = \frac{1}{3}$ and $P (red) = \frac{2}{3}$ . Since we can only either chose blue or red (exhaustive) and we cannot choose both at the same time (mutually exclusive), choosing blue and choosing red are complementary events, and $P (blue) + P (red) = 1$ .

Finally, let’s examine a non-example of complementary events. If you were asked to choose any number, you might think that that number could either be prime or composite. Clearly, a number cannot be both prime and composite, so that takes care of the mutually exclusive property. However, being prime or being composite are not exhaustive because the number 1 in mathematics is designated as “unique. ”

Attributions

Fundamentals of Probability
- “Boundless.”
  http://www.boundless.com/.
  Boundless Learning
  CC BY-SA 3.0.
- “Probability axioms.”
  http://en.wikipedia.org/wiki/Probability_axioms.
  Wikipedia
  CC BY-SA 3.0.
- “sample space.”
  http://en.wiktionary.org/wiki/sample_space.
  Wiktionary
  CC BY-SA 3.0.
- “disjoint.”
  http://en.wiktionary.org/wiki/disjoint.
  Wiktionary
  CC BY-SA 3.0.
- “independent.”
  http://en.wiktionary.org/wiki/independent.
  Wiktionary
  CC BY-SA 3.0.
- “Nuvola apps atlantik.”
  http://en.wikipedia.org/wiki/File:Nuvola_apps_atlantik.png.
  Wikipedia
  CC BY-SA.
Conditional Probability
- “Boundless.”
  http://www.boundless.com/.
  Boundless Learning
  CC BY-SA 3.0.
- “Bayes’ theorem.”
  http://en.wikipedia.org/wiki/Bayes’_theorem.
  Wikipedia
  CC BY-SA 3.0.
- “Conditional probability.”
  http://en.wikipedia.org/wiki/Conditional_probability.
  Wikipedia
  CC BY-SA 3.0.
- “conditional probability.”
  http://en.wiktionary.org/wiki/conditional_probability.
  Wiktionary
  CC BY-SA 3.0.
- “independent.”
  http://en.wiktionary.org/wiki/independent.
  Wiktionary
  CC BY-SA 3.0.
Unions and Intersections
- “Boundless.”
  http://www.boundless.com/.
  Boundless Learning
  CC BY-SA 3.0.
- “Union (set theory).”
  http://en.wikipedia.org/wiki/Union_(set_theory).
  Wikipedia
  CC BY-SA 3.0.
- “disjoint.”
  http://en.wiktionary.org/wiki/disjoint.
  Wiktionary
  CC BY-SA 3.0.
- “Intersection (set theory).”
  http://en.wikipedia.org/wiki/Intersection_(set_theory).
  Wikipedia
  CC BY-SA 3.0.
- “independent.”
  http://en.wiktionary.org/wiki/independent.
  Wiktionary
  CC BY-SA 3.0.
- “Venn0111.”
  http://en.wikipedia.org/wiki/File:Venn0111.svg.
  Wikipedia
  CC BY-SA.
- “Venn0001.”
  http://en.wikipedia.org/wiki/File:Venn0001.svg.
  Wikipedia
  CC BY-SA.
Complementary Events
- “Boundless.”
  http://www.boundless.com/.
  Boundless Learning
  CC BY-SA 3.0.
- “Complementary event.”
  http://en.wikipedia.org/wiki/Complementary_event.
  Wikipedia
  CC BY-SA 3.0.
- “mutually exclusive.”
  http://en.wiktionary.org/wiki/mutually_exclusive.
  Wiktionary
  CC BY-SA 3.0.
- “exhaustive.”
  http://en.wiktionary.org/wiki/exhaustive.
  Wiktionary
  CC BY-SA 3.0.
- “Heads or tails.”
  http://commons.wikimedia.org/wiki/File:Heads_or_tails.jpg.
  Wikimedia
  CC BY-SA.

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Boundless Statistics for Organizations Copyright © 2021 by Brad Griffith and Lisa Friesen is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

8.1: What Are the Chances?

8.1.1: Fundamentals of Probability

Key Points

Key Terms

Probability Rules

Extension of the Example

8.1.2: Conditional Probability

Key Points

Key Terms

Probability of B Given That A Has Occurred

Independence

Bayes’ Theorem

8.1.3: Unions and Intersections

Key Points

Key Terms

Union

Union of Two Sets

Intersection

8.1.4: Complementary Events

Key Points

Key Terms

What are Complementary Events?

Simple Examples

Attributions

License

Share This Book