8.3 More About Chance
8.3: More About Chance
8.3.1: The Paradox of the Chevalier De Méré
de Méré observed that getting at least one 6 with 4 throws of a die was more probable than getting double 6’s with 24 throws of a pair of dice.
Learning Objective
Explain Chevalier de Méré’s Paradox when rolling a die
Key Takeaways
Key Points
- Chevalier de Méré originally thought that rolling a 6 in 4 throws of a die was equiprobable to rolling a pair of 6’s in 24 throws of a pair of dice.
- In practice, he would win the first bet more than half the time, but lose the second bet more than half the time.
- de Méré asked his mathematician friend, Pascal, to help him solve the problem.
- The probability of rolling a 6 in 4 throws is
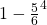, which turns out to be just over 50%. - The probability of rolling two 6’s in 24 throws of a pair of dice is
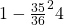, which turns out to be just under 50%.
Key Terms
- veridical paradox
- a situation in which a result appears absurd but is demonstrated to be true nevertheless
- independent event
- the fact that $A$ occurs does not affect the probability that $B$ occurs
- equiprobable
- having an equal chance of occurring mathematically
Chevalier de Méré
Antoine Gombaud, Chevalier de Méré (1607 – 1684) was a French writer, born in Poitou. Although he was not a nobleman, he adopted the title Chevalier (Knight) for the character in his dialogues who represented his own views (Chevalier de Méré because he was educated at Méré). Later, his friends began calling him by that name.
Méré was an important Salon theorist. Like many 17th century liberal thinkers, he distrusted both hereditary power and democracy. He believed that questions are best resolved in open discussions among witty, fashionable, intelligent people.
He is most well known for his contribution to probability. One of the problems he was interested in was called the problem of points. Suppose two players agree to play a certain number of games — say, a best-of-seven series — and are interrupted before they can finish. How should the stake be divided among them if, say, one has won three games and the other has won one?
Another one of his problems has come to be called “De Méré’s Paradox,” and it is explained below.
De Mere’s Paradox
Which of these two is more probable:
- Getting at least one six with four throws of a die or
- Getting at least one double six with 24 throws of a pair of dice?
The self-styled Chevalier de Méré believed the two to be equiprobable, based on the following reasoning:
- Getting a pair of sixes on a single roll of two dice is the same probability of rolling two sixes on two rolls of one die.
- The probability of rolling two sixes on two rolls is 1/6 as likely as one six in one roll.
- To make up for this, a pair of dice should be rolled six times for every one roll of a single die in order to get the same chance of a pair of sixes.
- Therefore, rolling a pair of dice six times as often as rolling one die should equal the probabilities.
- So, rolling 2 dice 24 times should result in as many double sixes as getting one six with throwing one die four times.
However, when betting on getting two sixes when rolling 24 times, Chevalier de Méré lost consistently. He posed this problem to his friend, mathematician Blaise Pascal, who solved it.
Explanation
Throwing a die is an experiment with a finite number of equiprobable outcomes. There are 6 sides to a die, so there is
probability for a 6 to turn up in 1 throw. That is, there is a 
probability for a 6 not to turn up. When you throw a die 4 times, the probability of a 6 not turning up at all is 
. So, there is a probability of 
of getting at least one 6 with 4 rolls of a die. If you do the arithmetic, this gives you a probability of approximately 0.5177, or a favorable probability of a 6 appearing in 4 rolls.
Now, when you throw a pair of dice, from the definition of independent events, there is a 
probability of a pair of 6’s appearing. That is the same as saying the probability for a pair of 6’s not showing is 35/36. Therefore, there is a probability of 
of getting at least one pair of 6’s with 24 rolls of a pair of dice. If you do the arithmetic, this gives you a probability of approximately 0.4914, or a favorable probability of a pair of 6’s not appearing in 24 rolls.
This is a veridical paradox. Counter-intuitively, the odds are distributed differently from how they would be expected to be.
de Méré’s Paradox
de Méré observed that getting at least one 6 with 4 throws of a die was more probable than getting double 6’s with 24 throws of a pair of dice.
8.3.2: Are Real Dice Fair?
A fair die has an equal probability of landing face-up on each number.
Learning Objective
Infer how dice act as a random number generator
Key Takeaways
Key Points
- Regardless of what it is made out of, the angle at which the sides connect, and the spin and speed of the roll, a fair die gives each number an equal probability of landing face-up. Every side must be equal, and every set of sides must be equal.
- The result of a die roll is determined by the way it is thrown; they are made random by uncertainty due to factors like movements in the thrower’s hand. Thus, they are a type of hardware random number generator.
- Precision casino dice have their pips drilled, then filled flush with a paint of the same density as the material used for the dice, such that the center of gravity of the dice is as close to the geometric center as possible.
- A loaded, weighted, or crooked die is one that has been tampered with to land with a specific side facing upwards more often than it normally would.
Key Terms
- random number
- number allotted randomly using suitable generator (electronic machine or as simple “generator” as die)
- pip
- one of the spots or symbols on a playing card, domino, die, etc.
- Platonic solid
- any one of the following five polyhedra: the regular tetrahedron, the cube, the regular octahedron, the regular dodecahedron and the regular icosahedron
A die (plural dice) is a small throw-able object with multiple resting positions, used for generating random numbers. This makes dice suitable as gambling devices for games like craps, or for use in non-gambling tabletop games.
An example of a traditional die is a rounded cube, with each of its six faces showing a different number of dots (pips) from one to six. When thrown or rolled, the die comes to rest showing on its upper surface a random integer from one to six, each value being equally likely. A variety of similar devices are also described as dice; such specialized dice may have polyhedral or irregular shapes and may have faces marked with symbols instead of numbers. They may be used to produce results other than one through six. Loaded and crooked dice are designed to favor some results over others for purposes of cheating or amusement.
What Makes Dice Fair?
A fair die is a shape that is labelled so that each side has an equal probability of facing upwards when rolled onto a flat surface, regardless of what it is made out of, the angle at which the sides connect, and the spin and speed of the roll. Every side must be equal, and every set of sides must be equal.
The result of a die roll is determined by the way it is thrown, according to the laws of classical mechanics; they are made random by uncertainty due to factors like movements in the thrower’s hand. Thus, they are a type of hardware random number generator. Perhaps to mitigate concerns that the pips on the faces of certain styles of dice cause a small bias, casinos use precision dice with flush markings.
Precision casino dice may have a polished or sand finish, making them transparent or translucent, respectively. Casino dice have their pips drilled, then filled flush with a paint of the same density as the material used for the dice, such that the center of gravity of the dice is as close to the geometric center as possible. All such dice are stamped with a serial number to prevent potential cheaters from substituting a die.
The most common fair die used is the cube, but there are many other types of fair dice. The other four Platonic solids are the most common non-cubical dice; these can make for 4, 8, 12, and 20 faces . The only other common non-cubical die is the 10-sided die.
Platonic Solids as Dice
A Platonic solids set of five dice; tetrahedron (four faces), cube/hexahedron (six faces), octahedron (eight faces), dodecahedron (twelve faces), and icosahedron (twenty faces).
Loaded Dice
A loaded, weighted, or crooked die is one that has been tampered with to land with a specific side facing upwards more often than it normally would. There are several methods for creating loaded dice; these include round and off-square faces and (if not transparent) weights. Tappers have a mercury drop in a reservoir at the center, with a capillary tube leading to another reservoir at a side; the load is activated by tapping the die so that the mercury travels to the side.
Attributions
- The Paradox of the Chevalier De Méré
- Are Real Dice Fair?
