18 Chi-square
Learning Outcomes
In this chapter, you will learn how to:
- Identify when appropriate to run a chi-square test of goodness-of-fit for independence.
- Describe the concept of a contingency table for categorical data.
- Complete hypothesis test for chi-square test of goodness-of-fit and independence.
- Compute and interpret effect size for chi-square.
- Describe Simpson’s paradox and why it is important for categorical data analysis.
We come at last to our final statistic: chi-square (χ2). This test is a special form of analysis called a nonparametric test, so the structure of it will look a little bit different from what we have done so far. However, the logic of hypothesis testing remains unchanged. The purpose of chi-square is to understand the frequency distribution of a single categorical variable or find a relationship between two categorical variables, which is a frequently very useful way to look at our data.
Categories and Frequency Tables
Our data for the χ2 test are categorical, specifically nominal, variables. Recall from Unit 1 that nominal variables have no specified order and can only be described by their names and the frequencies with which they occur in the dataset. Thus, unlike our other variables that we have tested, we cannot describe our data for the χ2 test using means and standard deviations. Instead, we will use frequencies tables.
|
|
Cat |
Dog |
Other |
Total |
|
Observed |
14 |
17 |
5 |
36 |
|
Expected |
12 |
12 |
12 |
36 |
Table 1. Pet Preferences
Table 1 gives an example of a frequency table used for a χ2 test. The columns represent the different categories within our single variable, which in this example is pet preference. The χ2 test can assess as few as two categories, and there is no technical upper limit on how many categories can be included in our variable, although, as with ANOVA, having too many categories makes our computations long and our interpretation difficult. The final column in the table is the total number of observations, or N. The χ2 test assumes that each observation comes from only one person and that each person will provide only one observation, so our total observations will always equal our sample size.
There are two rows in this table. The first row gives the observed frequencies of each category from our dataset; in this example, 14 people reported preferring cats as pets, 17 people reported preferring dogs, and 5 people reported preferring a different animal. The second row gives expected values; expected values are what would be found if each category had equal representation. Note: Chi-square tests should not be used when an expected value for any cell will be less than 5.
Calculation for Expected Value
[latex]E=\frac{N}{C}[/latex]
Where:
[latex]E=[/latex] the expected value or what we would expect if there was no preference or the preferences were equal
[latex]N=[/latex] the total number of people in our sample
[latex]C=[/latex] the number of categories in our variable (also the number of columns in our table, not including the Total column)
The expected values correspond with the null hypothesis for χ2 tests: equal representation of categories. Our first of two χ2 tests, the Goodness-of-Fit test, will assess how well our data lines up with, or deviates from, this assumption.
Goodness-of-Fit Test
The first of our two χ2 tests assesses one categorical variable against a null hypothesis of equally sized frequencies. Equal frequency distributions are what we would expect to get if placement into a particular category was completely random. We could, in theory, also test against a specific distribution of category sizes if we have a good reason to (e.g., we have a solid foundation of how the regular population is distributed), but this is less common, so we will not deal with it in this text. For example, if you know that for every 2 cats available for adoption there are 5 dogs available, you might expect more dogs than cats in your expected values row.
Step 1 - State the Hypotheses
All χ2 tests, including the goodness-of-fit test, are nonparametric. This means that there is no population parameter we are estimating or testing against; we are working only with our sample data. Because of this, there are no mathematical statements for χ2 hypotheses. This should make sense because the mathematical hypothesis statements were always about population parameters (e.g., μ), so if our test is nonparametric, we have no parameters and therefore no statistical notation hypothesis statements.
We do, however, still state our hypotheses in written form. For goodness-of-fit χ2 tests, our null hypothesis is that there is an equal number of observations in each category. That is, there is no difference between the categories in how prevalent they are. Our alternative hypothesis says that the categories do differ in their frequency. We do not have specific directions or one-tailed tests for χ2, matching our lack of mathematical statement. That is:
H0: There is not difference in number of observations between categories
HA: There is a difference in number of observations between categories
Step 2 - Find the Critical Value
Our degrees of freedom for the χ2 test are based on the number of categories we have in our variable, not on the number of people or observations like it was for our other tests. Luckily, they are still as simple to calculate.
Degrees of Freedom for χ2 Goodness of Fit Test
[latex]df=C-1[/latex]
So for our pet preference example, we have 3 categories, so we have 3-1=2 degrees of freedom. Our degrees of freedom, along with our significance level (still defaulted to α = 0.05) are used to find our critical values in a χ2 table, which is shown in Figure 1. Because we do not have directional hypotheses for χ2 tests (notice the number is a squared value so it can never be negative), we do not need to differentiate between critical values for 1- or 2-tailed tests. Just like our F tests for regression and ANOVA, all χ2 tests are 1-tailed tests. According Figure 1, our critical value would be χ2crit= 5.99.
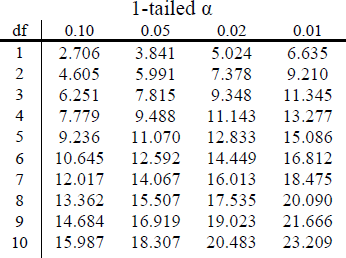
Figure 1. First 10 rows of a χ2 table
Step 3 - Calculate the Test Statistic
The calculations for our test statistic in χ2 tests combine our information from our observed frequencies (O) and our expected frequencies (E) for each level of our categorical variable. For each cell (category) we find the difference between the observed and expected values, square them, and divide by the expected values. We then sum this value across cells for our test statistic.
χ2 Goodness of Fit Test Statistic
[latex]\chi^2=\sum\frac{(O-E)^2}{E}[/latex]
Where:
[latex]O=[/latex] the observed frequency for a category
[latex]E=[/latex] the expected frequency for a category
If we do this for our pet preference data, we would have the following.
|
|
Cat |
Dog |
Other |
Total |
|
Observed |
14 |
17 |
5 |
36 |
|
Expected |
12 |
12 |
12 |
36 |
Table 2. Pet Preferences
[latex]\chi^2=\frac{(14-12)^2}{12}+\frac{(17-12)^2}{12}+\frac{(5-12)^2}{12}[/latex]
[latex]\chi^2=0.33+2.08+4.08=6.49[/latex]
Step 4 - Make a Decision and Interpret the Results
Now we can compare the test statistic of 6.49 to the critical value of 5.99. Because 6.49 is greater than 5.99, we can reject the null hypothesis and state that pet preference is different from random chance. So, let's interpret this in APA style.
The sample of 36 people showed a significant preference for type of pet, χ2(2) = 6.49, p < .05.
Finding a Relationship between Two Categorical Variables
An example contingency table is shown in Table 3 which displays whether or not 168 college students watched college sports growing up (Yes/No) and whether the students’ final choice of which college to attend was influenced by the college’s sports teams (Yes – Primary, Yes – Somewhat, No).
|
College Sports |
Affected Decision |
|
|||
|
Primary |
Somewhat |
No |
Total |
||
|
Watched |
Yes |
47 |
26 |
14 |
87 |
|
No |
21 |
23 |
37 |
81 |
|
|
|
Total |
68 |
49 |
51 |
168 |
Table 3. Contingency table of college sports and decision making
In contrast to the frequency table for our goodness-of-fit test, our contingency table does not contain expected values, only observed data. Within our table, wherever our rows and columns cross, we have a "cell". A cell contains the frequency of observing its corresponding specific levels of each variable at the same time. The top left cell in table 3 shows us that 47 people in our study watched college sports as a child AND had college sports as their primary deciding factor in which college to attend.
Cells are numbered based on which row they are in (rows are numbered top to bottom) and which column they are in (columns are numbered left to right). We always name the cell using (R, C), with the row first and the column second. Based on this convention, the top left cell containing our 47 participants who watched college sports as a child and had sports as a primary criteria is cell (1, 1). Next to it, which has 26 people who watched college sports as a child but had sports only somewhat affect their decision, is cell (1, 2), and so on. We only number the cells where our categories cross. We do not number our total cells, which have their own special name: marginal values. Marginal values are the total values for a single category of one variable, added up across levels of the other variable. In table 3, these marginal values have been italicized for ease of explanation, though this is not normally the case. We can see that, in total, 87 of our participants (47+26+14) watched college sports growing up and 81 (21+23+37) did not. The total of these two marginal values is 168, the total number of people in our study. Likewise, 68 people used sports as a primary criteria for deciding which college to attend, 50 considered it somewhat, and 50 did not use it as criteria at all. The total of these marginal values is also 168, our total number of people. The marginal values for rows and columns will always both add up to the total number of participants, N, in the study. If they do not, then a calculation error was made and you must go back and check your work.
Expected Values of Contingency Tables
Our expected values for contingency tables are based on the same logic as they were for frequency tables, but now we must incorporate information about how frequently each row and column was observed (the marginal values) and how many people were in the sample overall (N) to find what random chance would have made the frequencies out to be.
Calculating Expected Values for Contingency Tables
[latex]E=\frac{n_c*n_r}{N}[/latex]
Where:
[latex]n_c=[/latex] the number of people in the column
[latex]n_r=[/latex] the number of people in the row
[latex]N=[/latex] the total number of people in the entire sample
So, for our data we would calculate expected values for each cell of observed values as follows.
|
College Sports |
Affected Decision |
|
|||
|
Primary |
Somewhat |
No |
Total |
||
|
Watched |
Yes |
[latex]\frac{87*68}{168}[/latex] [latex]=35.21[/latex] |
[latex]\frac{87*49}{168}[/latex] [latex]=25.38[/latex] |
[latex]\frac{87*51}{168}[/latex] [latex]=26.41[/latex] |
87 |
|
No |
[latex]\frac{81*68}{168}[/latex] [latex]=32.79[/latex] |
[latex]\frac{81*49}{168}[/latex] [latex]=23.62[/latex] |
[latex]\frac{81*51}{168}[/latex] [latex]=24.59[/latex] |
81 |
|
|
|
Total |
68 |
49 |
51 |
168 |
Table 4. Contingency table of expected value calculations (with observed totals included for calculations) of college sports and decision making
Notice that the marginal values still add up to the same totals as before. This is because the expected frequencies are just row and column averages simultaneously. Our total N will also add up to the same value.
χ2 Test for Independence
The χ2 test performed on contingency tables is known as the test for independence. In this analysis, we are looking to see if the values of each categorical variable (that is, the frequency of their levels) is related to or independent of the values of the other categorical variable. Let's do the four-step test for this example.
Step 1 - State the Hypotheses
Because we are still doing a χ2 test which is nonparametric, we still do not have statistical versions of our hypotheses. The actual interpretations of the hypotheses are quite simple: the null hypothesis says that the variables are independent or not related, and alternative says that they are not independent or that they are related.
H0: Watching college sports as a child is not related to choosing college.
OR
H0: Watching college sports as a child is independent of college choice.
HA: Watching college sports as a child is related to choosing college.
OR
HA: Watching college sports as a child is not independent of college choice.
Step 2 - Find the Critical Value
For step 2, the only change is degrees of formula. Our critical value will come from the same table that we used for the goodness-of-fit test, but our degrees of freedom will change. Because we now have rows and columns (instead of just columns) our new degrees of freedom is found by multiplying two numbers together.
Degrees of Freedom for Test for Independence
[latex]df=(R-1)(C-1)[/latex]
Where:
[latex]R=[/latex] the number of rows in the contingency table (or the number of categories in the first categorical variable)
[latex]C=[/latex] the number of columns in the contingency table (or the number of categories in the second categorical variable)
So, for our example, we have
[latex]df=(2-1)(3-1)=1*2=2[/latex]
If we go back to Figure 1 and look at df = 2 for α = .05, we get a critical value of 5.99 again.
Step 3 - Calculate the Test Statistic
As you can see below, we calculate our test statistic for the test for independence the same way we did for the goodness of fit test. Our equation just gets a bit longer because we now have to do it for every cell in the contingency table. So, for our 2x3 contingency table, we will have 6 components in our equation.
Test for Independence Test Statistic
[latex]E=\frac{n_c*n_r}{N}[/latex]
Where:
[latex]n_c=[/latex] the number of people in the column
[latex]n_r=[/latex] the number of people in the row
[latex]N=[/latex] the total number of people in the entire sample
|
College Sports |
Affected Decision |
|
|||
|
Primary |
Somewhat |
No |
Total |
||
|
Watched |
Yes |
47 |
26 |
14 |
87 |
|
No |
21 |
23 |
37 |
81 |
|
|
|
Total |
68 |
49 |
51 |
168 |
Table 5. Contingency table with observed (and expected) values of college sports and decision making
With the observed and expected values found in Table 5, we can calculate our χ2 test statistic for this example.
[latex]\chi^2=\frac{(35.21-47)^2}{35.21}+\frac{(25.38-26)^2}{25.38}+\frac{(26.41-14)^2}{26.41}+\frac{(32.79-21)^2}{32.79}+\frac{(23.62-23)^2}{23.62}+\frac{(24.59-37)^2}{24.59}[/latex]
[latex]\chi^2=3.94+0.02+5.83+4.24+0.02+6.26=20.31[/latex]
Step 4 - Make a Decision and Interpret the Results
Reject H0. Based on our data from 168 people, we can say that there is a statistically significant relationship between whether or not someone watches college sports growing up and how much a college’s sports team factor in to that person’s decision on which college to attend, χ2(2) = 20.31, p < 0.05.
Effect Size for χ2
Like all other significance tests, χ2 tests – both goodness-of-fit and tests for independence – have effect sizes that can and should be calculated for statistically significant results. There are many options for which effect size to use, and the ultimate decision is based on the type of data, the structure of your frequency or contingency table, and the types of conclusions you would like to draw. For the purpose of our introductory course, we will focus only on a single effect size that is simple and flexible: Cramer’s V. This is appropriate to use when the χ2 test involves a matrix larger that 2 X 2. Cramer’s Vis a type of correlation coefficient that can be computed on categorical data.
Cramer's V
[latex]V=\sqrt{\frac{\chi^2}{N(k-1)}}[/latex]
Where:
[latex]N=[/latex] the total number of people in the sample
[latex]k=[/latex] the smaller value of either R (the number of rows) or C (the number of columns, that is the number of categories for the variable with the smallest number of categories
[latex]\chi^2=[/latex] the test statistic calculated in Step 4
So, for our example above, we can calculate an effect size given that we found a significant relationship and that we have a 2x3 contingency table that we are working with.
We know that N = 168 and k would either be 2 or 3, but we want the smaller of the two, so k = 2. And, finally, χ2 = 20.31.
[latex]V=\sqrt{\frac{20.31}{168(2-1)}}=\sqrt{\frac{20.31}{168}}=\sqrt{0.121}=0.35[/latex]
Like other statistic effect sizes there are range cut offs of small, medium, and large. So the statistically significant relation between our variables was moderately strong examining the effect size table below.
| Small | Medium | Large | |
| df = 1 | 0.10 | 0.30 | 0.50 |
| df = 2 | 0.07 | 0.21 | 0.35 |
| df = 3 | 0.06 | 0.17 | 0.29 |
Table 6. The effect size ranges of Cramer’s V.
Additional Thoughts
Beyond Pearson's Chi-Square Test: Standardized Residuals
For a more applicable example, let’s take the question of whether a Black driver is more likely to be searched when they are pulled over by a police officer, compared to a white driver. The Stanford Open Policing Project (https://openpolicing.stanford.edu/) has studied this, and provides data that we can use to analyze the question. We will use the data from the State of Connecticut since they are fairly small and thus easier to analyze.
The standard way to represent data from a categorical analysis is through a contingency table, which presents the number or proportion of observations falling into each possible combination of values for each of the variables. Table 7 below shows the contingency table for the police search data. It can also be useful to look at the contingency table using proportions rather than raw numbers, since they are easier to compare visually, so we include both absolute and relative numbers here.
| searched | Black | White | Black (relative) | White (relative) |
|---|---|---|---|---|
| FALSE | 36244 | 239241 | 0.13 | 0.86 |
| TRUE | 1219 | 3108 | 0.00 | 0.01 |
Table 7. Contingency Table for Police Search Data
The Pearson chi-squared test (discussed above) allows us to test whether observed frequencies are different from expected frequencies, so we need to determine what frequencies we would expect in each cell if searches and race were unrelated – which we can define as being independent. If we perform this test easily using our statistical software, X2 (1) = 828, p < .001. This shows that the observed data would be highly unlikely if there was truly no relationship between race and police searches, and thus we should reject the null hypothesis of independence.
When we find a significant effect with the chi-squared test, this tells us that the data are unlikely under the null hypothesis, but it doesn’t tell us how the data differ. To get a deeper insight into how the data differ from what we would expect under the null hypothesis, we can examine the residuals from the model, which reflects the deviation of the data (i.e., the observed frequencies) from the model (i.e., the expected frequencies) in each cell. Rather than looking at the raw residuals (which will vary simply depending on the number of observations in the data), it’s more common to look at the standardized residuals (sometimes called Pearson residuals).
Table 8 shows these for the police stop data from X2 above. Remember that we examined the question of whether a Black driver is more likely to be searched when they are pulled over by a police officer, compared to a white driver. These standardized residuals can be interpreted as Z scores – in this case, we see that the number of searches for Black individuals are substantially higher than expected based on independence, and the number of searches for white individuals are substantially lower than expected. This provides us with the context that we need to interpret the significant chi-squared result.
| searched | driver_race | Standardized residuals |
|---|---|---|
| FALSE | Black | -3.3 |
| TRUE | Black | 26.6 |
| FALSE | White | 1.3 |
| TRUE | White | -10.4 |
Table 8. Summary of standardized residuals for police stop data
Beware of Simpson’s paradox
The contingency tables that represent summaries of large numbers of observations, but summaries can sometimes be misleading. Let’s take an example from baseball. The table below shows the batting data (hits/at bats and batting average) for Derek Jeter and David Justice over the years 1995-1997:
| Player | 1995 | 1996 | 1997 | Combined | ||||
|---|---|---|---|---|---|---|---|---|
| Derek Jeter | 12/48 | .250 | 183/582 | .314 | 190/654 | .291 | 385/1284 | .300 |
| David Justice | 104/411 | .253 | 45/140 | .321 | 163/495 | .329 | 312/1046 | .298 |
Table 9. Player Batting data for 2 baseball players
If you look closely, you will see that something odd is going on: In each individual year Justice had a higher batting average than Jeter, but when we combine the data across all three years, Jeter’s average is actually higher than Justice’s! This is an example of a phenomenon known as Simpson’s paradox, in which a pattern that is present in a combined dataset may not be present in any of the subsets of the data. This occurs when there is another variable that may be changing across the different subsets – in this case, the number of at-bats varies across years, with Justice batting many more times in 1995 (when batting averages were low). We refer to this as a lurking variable, and it’s always important to be attentive to such variables whenever one examines categorical data.
describing any analytic method that does not involve making assumptions about the data of interest.
a two-dimensional table in which frequency values for categories of one variable are presented in the rows and values for categories of a second variable are presented in the columns: Values that appear in the various cells then represent the number or percentage of cases that fall into the two categories that intersect at this point.
In a contingency table, the total values for a single category of one variable, added up across levels of the other variable
a procedure used to test the hypothesis of the relationship between two categorical variables. The observed frequencies of a variable are compared with the frequencies that would be expected if the null hypothesis of no association (i.e., statistical independence) were true.

