MEASUREMENT

Tulsa Community College

3 MEASUREMENT

Learning Objectives

Test predictions from scientific hypotheses using basic biological laboratory techniques.
Identify accurate measures with a variety of laboratory instruments.
Convert measures using with metric system and scientific notation.

Activity

What are the conversions for the following measurements?
1. 550 ml = ____ L
2. 12 g = ____ mg
3. 800 μl = ____ ml
4. 1 gallon = ____ pints
5. 7000 ml = ____ L
Visit the weighing station. What is the weight of a weighing boat? Some balances have a method of subtracting it by pressing the “zero” or “tare” button. Weigh three items. Record the results.
Discuss the answers to questions 1 and 2 with the group.

Measurement

In the lab, you will need to use instruments to make your measurements. There are instruments to use for each type of substance (liquid or solid). Some of the instruments to measure volume are graduated cylinders (shown in Figure 1.2) and pipettes (shown in Figure 1.3 and Figure 1.4). Some instruments to measure solids are balances and scales (a scale is shown in Figure 1.5). You may also need to adjust the instrument or container you are using based on the amount of substance you need to measure.

Also, when recording your measurements in a data table, it is important to be aware of significant figures. The number of significant figures is the number of digits needed to express the accuracy of a calculation. The rules for significant figures are presented in Figure 1.5. To use these rules, let’s look at an example. An experiment requires you to measure the weight of 10 marbles. The scale shows a weight of 32.46547g. All the digits in this measurement are significant figures. However, in the number 32.465470, how do we know if the last 0 is significant or not? There are three rules on how to determine significant figures:

Non-zero digits are always significant.
Any zeros between two significant digits are significant.
A final zero or trailing zeros in the decimal portion only are significant.

So, based on this rule, the final zero in 32.465470 is significant, as is the first zero in 32.046570. However, the zero in 0.324657 would not be significant because it is simply a placeholder.

Safety Precautions

Inform your teacher immediately of any broken glassware, as it could cause injuries.
Clean up any spilled fluids to prevent other people from slipping.
Wash your hands with soap and water after completion of the activity.

For this activity, you will need the following:

A balance
A weighing boat
A graduated cylinder
Weighable objects

For this activity, you will work in pairs.

Structured Inquiry

Step 1: Create a data table for your measurements and show your calculations on your lab paper.

Step 2: Hypothesize/Predict: Examine one of the objects. Predict the object’s mass and write the predicted mass on your paper.

Step 3: Student-Led Planning: Listen to your teacher’s instructions on how to use the balance. Discuss with your partner how you should determine the weight of the object and how many significant figures your measurement should have. Write your ideas on your paper.

Step 4: Determine the weight of the object using the scale. Repeat the measurement twice more and record all results on your paper.

Step 5: Critical Analysis: How much did your measurements vary among the three trials? Were you able to accurately measure to the amount of significant figures stated in Step 3? Why or why not? Could you have improved your methods to get more accurate measurements or obtain a greater number of significant figures? Why or why not? Discuss with your partner, and then write your answers on your paper.

Click here to learn more about the displacement method of measurement.

Guided Inquiry

Step 1: Volume is a measure of how much space matter occupies, and it is used to calculate density (d) where m is the mass of the object and v is the object’s volume.

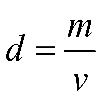
Formula of d (density) equals m (mass) divided by v (volume)

Pick another object available in your lab and predict whether it has a higher or lower density than the object you used during the Structured Inquiry. Write your prediction on your paper.

Step 2: How can you calculate the density of your two objects? Devise a plan for finding the density of both objects and present it to your teacher for approval. Create the data tables you need and decide how many times you should measure each object as well as how many significant figures you will use.

Step 3: After your teacher approves, take the measurements you need to calculate the density of both objects. Write your final densities on your paper.

Step 4: How did the object’s size influence its mass and its volume? What would you have to do to increase the mass, volume, and density of an object? How could you increase the accuracy of your measurements? Discuss with your partner, and then write your answers on your paper.

Assessment

Why do we subtract the weight of the weigh boat to accurately measure the weight of an object within the weighing boat?
What is instrument or vessel would be used to measure the following volumes accurately?
1. 200 ml
2. 50 μl
3. 1 L
Calculate the density of an object that is 3 g and that displaces water in a graduated cylinder by 3 ml.

SCIENTIFIC NOTATION

Quantities have two parts: the number and the unit. The number tells “how many.” It is important to be able to express numbers properly so that the quantities can be communicated properly.

Standard notation is the straightforward expression of a number. Numbers such as 17, 101.5, and 0.00446 are expressed in standard notation. For relatively small numbers, standard notation is fine. However, for very large numbers, such as 306,000,000, or for very small numbers, such as 0.000000419, standard notation can be cumbersome because of the number of zeros needed to place nonzero numbers in the proper position

Scientific notation is an expression of a number using powers of 10. Powers of 10 are used to express numbers that have many zeros:

Table shows the powers of 10. Left side has 10 to a specific power and right side has the equation for the specified power.
10⁰	= 1
10¹	= 10
10²	= 100 = 10 × 10
10³	= 1,000 = 10 × 10 × 10
10⁴	= 10,000 = 10 × 10 × 10 × 10

and so forth.

The raised number to the right of the 10 indicates the number of factors of 10 in the original number. (Scientific notation is sometimes called exponential notation.) The exponent’s value is equal to the number of zeros in the number expressed in standard notation.

Small numbers can also be expressed in scientific notation but with negative exponents:

Table shows the powers of 10 with negative exponents. Left side has 10 to a specific power and right side has the equation for the specified power.
10⁻¹	= 0.1 = 1/10
10⁻²	= 0.01 = 1/100
10⁻³	= 0.001 = 1/1,000
10⁻⁴	= 0.0001 = 1/10,000

and so forth. Again, the value of the exponent is equal to the number of zeros in the denominator of the associated fraction. A negative exponent implies a decimal number less than one.

A number is expressed in scientific notation by writing the first nonzero digit, then a decimal point, and then the rest of the digits. The part of a number in scientific notation that is multiplied by a power of 10 is called the coefficient. We determine the power of 10 needed to make that number into the original number and multiply the written number by the proper power of 10.

For example, to write 79,345 in scientific notation,

$79, 345 = 7.9345 \times 10, 000 = 7.9345 \times 10^{4}$

Thus, the number in scientific notation is

$7.9345 \times 10^{4}$ .

For small numbers, the same process is used, but the exponent for the power of 10 is negative:

0.000411 = 4.11 \times \frac{1}{10, 000} = 4.11 \times 10^{- 4}

Typically, the extra zero digits at the end or the beginning of a number are not included (Figure $2.2. 1$ ).

Figure $2.2. 1$

“The Blue Marble” is a famous photograph of the Earth taken on December 7, 1972, by the crew of the Apollo 17 spacecraft en route to the Moon at a distance of about 29,000 kilometers. This is

$2.9 \times 10^{4} k m.$

It shows Africa, Antarctica, and the Arabian Peninsula.The earth is about 93,000,000 miles from the sun. In scientific notation, this is

$9.3 \times 10^{7} m i l e s.$

(Public Domain; NASA/Apollo 17 crew; taken by either Harrison Schmitt or Ron Evans)

Assessment

Express these numbers in scientific notation.

366,000
0.00894
3,760,000
0.00000679
43,090
0.0004406

Many quantities in chemistry are expressed in scientific notation. When performing calculations, you may have to enter a number in scientific notation into a calculator. Be sure you know how to correctly enter a number in scientific notation into your calculator. Different models of calculators require different actions for properly entering scientific notation. If in doubt, consult your instructor immediately (Figure $2.2. 2$

Calculator shows number, 3.84951 to the 18th power — Figure $2.2. 2$

This calculator shows only the coefficient and the power of 10 to represent the number in scientific notation. Thus, the number being displayed is

$3.84951 \times 10^{18}$ or

$3, 849, 510, 000, 000, 000, 000$

Source: “Casio” Asim Bijarani is licensed under Creative Commons Attribution 2.0 Generic.

Exercises

Calculate the following:

8.639 x 10⁴ =
5.9921 x 10^-5 =
4.3042 x 10⁶ =

The Scientific Notation section of this chapter is adapted from Numbers In Measurement (Scientific Notation) which was authored, remixed, and/or curated by LibreTexts. Licensed CC BY NC SA.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License